BASHA TECH
4. 선형 연립 방정식의 해 본문
n개의 변수를 갖는 m개의 방정식으로 이루어진 것 => 선형 연립방정식

제차 연립방정식은 위 사진을 기준으로 하면, b가 싹 다 0인 것.
비제차 연립방정식은 m개의 b 중 하나라도 0이 아니면 됨.
1. 비제차 선형 연립 방정식
1) 역행렬 이용
2) 크래머 공식
3) 가우스-조단 소거법
2. 제차 선형 연립 일차방정식의 해
1) 제차 연립 방정식의 그래프 : 선형 연립 방정식의 그래프는 두 직선을 나탬, 그리고 두 직선은 무조건 원점을 지나는 직 선이다 (즉, y절편 = 0)
2) 제차 연립 방ㅈㅇ식의 해
1) ab - bc =/= 0 : 오직 하나 해 (자명한 해)
2) ab - bc = 0 : 무수히 많은 해 (부정) , 자명한 해 이외의 해를 갖는다.
3. 행렬의 계수 (rank)
1) 행렬의 계수 정의 : m x n 행렬 A의 1차 독립인 행벡터(열벡터)의 최대의 개수를 A의 계수(rank)라 함.
- 참고 : 일차 독립, 일차 종속
만약 벡터 공간 V의 부분집합 S에 대해 Ax = 0을 만족하는 유한개의 벡터 와 적어도 하나가 아닌 0이 아닌 스칼라 이 존재하면, 집합 S는 일차종속이며, S의 벡터 또한 일차종속이다.
임의의 벡터 에 대해 이면, 이다. 이를 의 일차결합에 대한 영벡터의 자명한 표현이라 한다.
다시말해, 어떤 집합이 일차 종속이라면 해당 집합에 속하는 벡터들을 이용해 영벡터를 자명하지 않은 표현으로 표현할 수 있다.
벡터 공간의 부분집합 S가 일차종속이 아니라면 일차독립이다
- rank 구하는 방법 : A를 기본 행 연산을 적용하여 사다리꼴 행렬을 만들었을 때 원소 중 적어도 하나가 0이 아닌 행의 개수가 rankA이다.

- rank 값의 특징 : m x n 행렬에서 행렬의 계수 (rank)는 행과 열 중에 작은 숫자보다 같거나 작다.
2) 행렬의 계수의 성질
4. 선형 연립 방정식의 해의 존재 유무
1) 선형 연립 방정식의 계수 행렬의 이용한 정보 : m은 방정식의 개수, n은 미지수의 개수
<첨가행렬>
mn개의 수를 m개의 행과 n개의 열로
배열한 것을 m×n 행렬(matrix)이라 한다.
행렬의 구조를 이용하여
연립일차방정식을 표현한다고 생각하자.
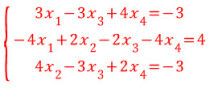
이 연립일차방정식의 계수와 상수항으로 된 행렬은

이 행렬을 연립일차방정식의 첨가행렬(augmented matrix)이라 한다.
m×n 연립일차방정식의 첨가행렬은 m×(n+1) 행렬이다.
위 첨가행렬에서 마지막 열을 삭제한
다음 행렬을 계수행렬(coefficient matrix)이라 한다.
2) 선형 연립 방정식의 해의 기하학적 의미
- 비제차 연립 방정식에서
=> 해가 오직 하나 존재 (한 점에서 만남), 해가 무수히 많이 존재 (일치), 해가 존재하지 않음 (평행)
3) 선형 연립 방정식의 해의 존재 유무 판단
- 해가 오직 하나 존재하는 경우
- 해가 무수히 많이 존재하는 경우 (부정)
- 해가 존재 하지 않는 경우 (불능)
5. 최소 제곱의 해 : 해는 존재 하지 않지만 해가 있다고 치고 ^x=(ATA)−1ATb을 이용하여 구한 해 ^x를 최소 제곱의 해라 함
6. 행사다리꼴 및 기약사다리꼴
1) 행사다리꼴
2) 기약 행 사다리꼴
7. LU-분해
'Math > 선형대수' 카테고리의 다른 글
| 6. 벡터의 내적 (0) | 2022.10.17 |
|---|---|
| 5. 벡터의 정의 및 연산 (0) | 2022.10.17 |
| 3. 행렬의 종류 (0) | 2022.10.13 |
| 2. 행렬식 (0) | 2022.10.13 |
| 1. 행렬의 정의와 연산 및 성질 (0) | 2022.10.13 |



