BASHA TECH
CH5. 머신러닝 복습 : 회귀 본문
1. 회귀 소개 : 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법. (오차가 minimize 되는 것을 찾는다.) 여러 개의 독립변수와 한 개의 종속변수 같의 상관관계를 모델링하는 기법을 통칭한다.


머신러닝 관점에서 보면 독립변수는 피처에 해당되며 종속변수는 결정 값이다. 따라서 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다.
회귀는 회귀 계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러 가지 유형으로 나눌 수 있다. 회귀에서 가장 중요한 것은 회귀 계수(w: weight)이다. 이 회귀 계수가 선형인지 아닌지에 따라 선형 회귀와 비선형 회귀로 나눌 수 있다. 그리고 독립변수의 개수가 한 개인지 여러 개인지에 따라 단일 회귀, 다중 회귀로 나뉜다.

지도학습은 2가지 유형으로 나뉘는데 그것은 분류와 회귀이다. 이 2가지 기번의 가장 큰 차이는 분류는 예측값이 카테고리와 같은 이산형 클래스 값이고, 회귀는 연속형 숫자값이라는 것이다.

선형 회귀는 실제 값과 예측 값의 차이 (오류의 제곱 값)을 최소화하는 직선형 회귀선을 최적화하는 방식이다. 선형 회귀 모델은 규제 방법에 따라서도 별도의 유형으로 나눌 수 있다. 규제는 일반적인 선형회귀의 과적합 문제를 해결하기 위해 회귀 계수 (w)에 패널티 값을 적용하는 것을 말한다.
대표적인 선형회귀 모델
- 일반 선형 회귀 : 예측값과 실제값의 RSS(Residual Sum of Squares)를 최소화 할 수 있도록 회귀 계수를 최적화 하며 규제를 적요하지 않은 모데
- 릿지(Ridge) : 릿지 회귀는 선형회귀에 L2 규제를 추가한 회귀 모델이다. 릿지 회귀는 L2 규제를 적용하는데 L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀 계수 값을 더 작게 만드는 규제 모델이다.
- 라쏘(Lasso) : 라쏘 회귀는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것이다. 이러한 특성 때문에 L1 규제는 피처 선택 기능으로도 불린다.
- 엘라스틱넷(ElasticNet) : L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터 세트에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정한다.
- 로지스틱 회귀(Logistic Regression) : 로지스틱 회귀는 회귀라는 이름이 붙어 있지만, 사실은 분류에 사용되는 선형 모델. 로지스틱 회귀는 매우 강력한 분류 알고리즘이다. 일반적으로 이진 분류뿐만 아니라 희소 영역의 분류. 예를 들어 텍스트 분류와 같은 영역에서 뛰어난 예측 성능을 보인다.
2. 단순 선형 회귀를 통한 회귀 이해
단순 선형 회귀는 독립 변수도 하나, 종속 변수도 하나인 선형 회귀다.

실제 값과 회귀 모델의 차이에 따른 오류 값을 남은 오류를 잔차라 부른다. 최적의 회귀 모델을 만든다는 것은 바로 전체 데이터의 잔차 합이 최소가 되는 모델을 만든다는 것을 의미한다. 동시에 오류 값 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는단은 의미도 된다.
오류 값은 + 도 - 가 될 수도 있다. 그래서 전체 데이터의 오류 합을 구하기 위해 단순히 더했다는 뜻하지 않게 오류 합이 크게 줄어들 수 있기 때문에 오류 합을 계산할 때는 절댓값을 취해서 더하거나 (Mean Absolute Error), 오류 값의 제곱을 구해서 더하는 방식 (RSS, Residual Sum of Square)을 취한다. 일반적으로 미분 등의 계산을 편리하기 위해 RSS 방식으로 오류 합을 구한다. 즉 Error의 제곱은 = RSS 이다.
RSS를 최소로 하는 회귀 계수를 학습을 통해서 찾는 것이 머신러닝 기반 회귀의 핵심이다. RSS는 회귀식의 독립변수 X, 종속변수 Y가 중신 변수가 아니라 w변수 (회귀 계수)가 중심 변수임을 인지하는 것이 매우 중요하다. (학습 데이터로 입력되는 독립변수와 종속변수는 RSS에서 모두 상수로 간주한다)

회귀에서 이 RSS는 비용(cost)이며, w변수(회귀 계수)로 구성되는 RSS를 비용함수라고 한다. 머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값 (오류값)을 지속해서 감소시키고 최종저긍로는 더 이상 감소하지 않는 최소의 오류값을 구하는 것이다. 비용 함수를 손실함수(loss function = costfunction) 라고도 한다. (최소화된 오차를 구하는 모델 => optimizer)
3. 경사 하강법 (Gradient Descent) - 비용 최소화하기
점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트 하면서 오류값이 최소가 되는 W 파라미터를 구하는 방식이다. 경사 하강법은 반복적으로 비용 함수의 반환 값. 즉, 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해나간다. 최초 오류값이 100이었다면 두번째 오류값은 90, 세번째는 80과 같은 방식으로 지속해서 오류를 감소시키는 방향으로 W값을 계속 업데이트해 나간다. 그리고 오류값이 더 이상 작아지지 않으면 그 오류 값을 최소비용으로 판단하고 그때의 W값을 최적 파라미터로 반환한다.
따라서 경사 하강법의 핵심은 "어떻게 하면 오류가 작아지는 방향으로 W값을 보정할 수 있을까?" 이다. 예를 들어 비용 함수가 다음 그림과 같은 포물선 형태의 2차 함수라면 경사 하강법은 최초 w 에서부터 미분을 적요한 뒤 이 미분 값이 계속 감소하는 방향으로 순착적으로 w를 업데이트 한다. 마침내 더이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그때의 w를 반환한다.
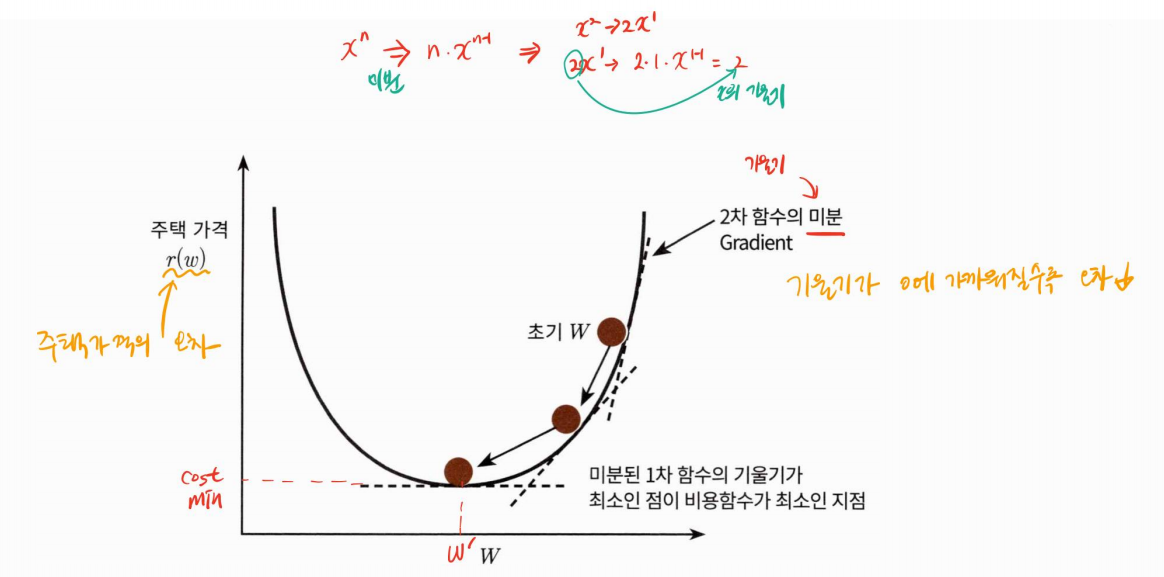

경사 하강법은 새로운 Wi = 이전
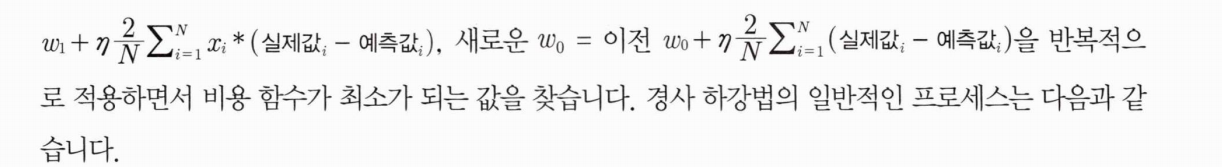

단순 선형 회귀로 예측할만한 데이터 세트 만들기
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y = 4X + 6을 근사 (w1 = 4, w0 = 6) 임의의 값은 노이즈를 위해 만듦.
X = 2 * np.random.rand(100,1)
y = 6 + 4 * X + np.random.randn(100, 1)
# X, y 데이터 세트 산점도로 시각화
plt.scatter(X, y)def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred)/N
return cost
경사 하강법 함수 생성 및 구현
# w1과 w0을 업데이트할 w1_update, w0_update를 반환
def get_weight_updates (w1, w0, X, y, learning_rate = 0.01):
N = len(y)
# 먼저 w1_update, w0_update를 각각 w1, w0의 shape과 동일한 크기를 가지 0 값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
# 예측 배열 계산하고 예측과 실제 값의 차이 계산
y_pred = np.dot(X, w1.T) + w0
diff = y - y_pred
# w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1.update, w0_update
get_weight_updates()를 경사 하강 방식으로 반복적으로 수행하여 w1과 w0을 업데이트 하는 함수 gradient_descent_steps() 함수 생성
# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1 과 w0를 업데이트 적용함.
def gradient_descent_steps(Xz y, iters=10000):
# w0과 w1을 모두 0으로 초기화
w0 = np.zeros((1, 1))
w1 = np.zeros((1, 1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출해 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
gradient_descent_steps를 호출해 w1, w0을 구하고 최종적으로 예측값과 실제값의 RSS차이를 계산하는 get_cost()함수를 생성하고 이를 이용해 경사 하강법의 예측 오류를 계산
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
printC'wl:{0:.3f} w0:{1:.3f}".format(w1 [0, 0], w0[0, 0]))
y_pred = w1 [0, 0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
4. LinearRegression 클래스 - Ordinary Least Squares (OLS)
LinearRegression 클래스는 예측값과 실제값의 RSS를 최소화해 OLS 추정 방식으로 구현한 클래스. LinearRegression 클래스는 fit() 메소드로 X, y 배열을 입력받으면 회귀 계수인 W를 coef_ 속성에 저장한다.
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)OLS 기반의 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받는다. 피처 간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 민감해진다. 이러한 현상을 다중 공선성(multi-collinearity) 문제라고 한다. 일반적으로 상관관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용한다. 또한 매우 많은 피처가 다중 공선성 문제를 가지고 있다면 PCA를 통해 차원 축소를 수행하는 것도 고려해볼 수 있다.
회귀 평가 지표
회귀의 평가를 위한 지표는 실제 값과 회귀 예측값을 기반으로 한 지표가 중심이다. 실제값과 예측값의 차이를 그냥 더하면 +와 -가 섞여서 오류가 상쇄된다. 이 때문에 오류의 절댓값 평균이나 제곱, 또는 제곱한 뒤 다시 루트를 씌운 평균값을 구한다.

하지만 사이킷런은 RMSE를 제공하지 않기 때문에 MSE에 제곱근을 씌워서 계산하는 함수를 직접 만들어야한다.

다항회귀
다항 회귀도 선형 회귀이다.
선형/비선형 회귀를 나누는 기준은 회귀 계수가 선형/비선형인지를 따르는 것이다. 독립변수의 선형/비선형 여부와는 무관.
다항 회귀를 이용한 과소적합 및 과적합 이해
다항 회귀는 피처의 직선적 관계가 아닌 복잡한 다항 관계를 모델링 할 수 있다. 다항식의 차수가 높아질수록 매우 복잡한 피처 간의 관계까지 모델링이 가능하다. 하지만 다항 회귀의 차수를 높일 수록 학습 데이터에만 너무 맞춘 학습이 이뤄져 테스트 데이터 환경에서의 예측 정확도가 떨어지는 과적합 문제가 발생한다.
편향-분산 트레이드 오프 (Bias-Variance Trade off)
저편향/저분산은 예측 결과가 실제 결과에 매우 잘 근접하면서도 예측 변동이 크지 않고 특정 부분에 집중 돼 있는 아주 뛰어난 성능을 보여준다.
저편향/고분산은 예측 결과가 실제 결과에 매우 잘 근접하지만 예측 결과가 실제 결과를 중심으로 꽤 넒은 부분에 분포되어 있다.
고편향/저분산은 정확한 결과에서 벗어나면서도 예측이 특정 부분에 집중되어있다.
고편향/고분산은 정확한 예측 결과를 벗어난면서도 넓은 부분에 분포해 있다.
일반적으로 편향과 분산은 한쪽이 높으면 한쪽이 낮아지는 경향이 있다. 즉, 편향이 높으면 분산은 낮아지고 (과소적합) 반대로 분산이 높으면 편향이 낮아진R다 (과적합)
편향이 너무 높으면 전체 오류가 높다. 편향을 점점 낮추면 동시에 분산이 높아지고 전체 오류도 낮아지게 된다. 편항을 낮추고 분산을 높이면서 전체 오류가 가장 낮아지는 골디락스 지점을 통과하면서 분산을 지속적으로 높이면 전체 오류값이 증가하면서 예측 성능이 저하된다.
높은 편향, 낮은 분산에서 과소적합되기 쉬며 낮은 편향.높은 분산에서 과적합 되기 쉽다.
편향과 분산이 서로 트레이드오프를 이루면서 오류 cost 값이 최대로 낮아지는 모델을 구축하는 것이 가장 효율적인 머신러닝 예측 모델을 만드는 방법이다,.
규제 선형 모델 - 릿지, 라쏘, 엘라스틱
- 규제선형 모델의 개요
이전의 선형 모델의 비용 함수는 RSS를 최소화하는 것만 고려했지만 학습 데이터에 지나치게 맞추게 되어 회귀계수가 쉽게 커지는 문제점이 발생. 이럴 경우 변동성이 오히려 심해져서 테스트 데이터 세트에서는 예측 성능이 저하되기 쉽다. 이를 반영해 비용 함수는 학습 데이터의 잔차 오류 값을 최소로 하는 RSS 최소화 방법과 과적합을 방지 하기 위해 회귀 계수 값이 커지지 않도록 하는 방법이 서로 균형을 이뤄야한다.
alpha를 0에서부터 지속적으로 값을 증가시키면 회귀 계수 값의 크기를 감소시킬 수 있다. 이처럼 비용 함수에 alpha 값으로 페널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 규제라고 부른다.
규제는 L1, L2 방식으로 구분된다. L2규제는 W의 제곱에 대해 페널티를 부여하는 방식을 말한다. L2 규제를 적용한 회귀는 릿지 회귀라 한다. L1규제는 W의 절댓값에 대해 페널티를 부여한다. L1규제를 적용하면 영향력이 크지 않은 회귀 계수 값을 0으로 변환한다. 이러한 L1 규제를 적용한 회귀를 릿지 회귀라 한다. L2 규제가 회귀 계수의 크기를 감소시키는데 반해 L1 규제는 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거한다. 이러한 측면에서 L1규제는 적절한 피처만 회귀에 포함 시키는 피처 선택의 특성을 가지고 있다.
- 릿지 회귀
- 라쏘 회귀
- 엘라스틱넷 회귀 : L1 + L2 규제를 결합한 회귀.
- 선형 회귀 모델을 위한 데이터 변환
선형 회귀 모델과 같은 선형 모델은 일반적으로 피처와 타깃값 간에 선형의 관계가 있다고 가정하고, 이러한 최적의 선형 함수를 찾아내 결괏값을 예측한다. 또한 선형 회귀 모델은 피처 값과 타깃 값의 분포가 정규 분포 (평균을 중심으로 종 모양으로 데이터 값이 분포된 형태) 형태를 매우 선호한다. 특히 타깃갑의 경우 정규 분포 형태가 아니라 특정 값의 분포가 치우진 왜곡 된 형태의 분포도일 경우 예측 성능에 부정적인 영향을 미칠 가능성이 높다. 피처값 역시 결정값보다는 덜하지만 왜곡된 분포도로 인해 예측 성능에 부정적인 영향을 미칠 수 있다. 따라서 선형 회귀 모델을 적용하기 전에 먼저 데이터에 대한 스케일링/정규화 작업을 하는 것이 일반적이이다. 하지만 이러한 작업을 선행한다고 해서 무조건 예측 성능이 향상되는 건 아니다. 일반적으로 중요 피처들이나 타깃값의 분포도가 심하게 왜곡 됐을 경우 이러한 변환 작업을 수행한다.
타깃 값의 경우는 일반적으로 로그변환을 적용한다. 결정값을 정규 분포나 다른 정규값으로 변환하면 변환된 값을 다시 원본 타깃값으로 원복하기 어려울 수 있다. 무엇보다도 왜곡된 분포도 형태의 타깃 값을 로그 변환하여 예측 성능 향상이 된 경우가 많은 사례에서 검증되었기 때문에 타깃값의 경우는 로그 변환을 적용한다.
일반적으로 선형 회귀를 적용하려는 데이터 세트에 데이터 값의 분포가 심하게 왜곡 되어 있을 경우에 로그변환을 적용하는 것이 좋은 결과를 기대할 수 있다.
로지스틱 회귀
선형 회귀 방식을 분류에 적용한 알고리즘. 즉, 분류에 사용된다.
회귀가 선형인가 비선형인가는 독립변수가 아닌 가중치 변수가 선형인지 아닌지를 따른다. 로지스틱 회귀가 선형 회귀와 다른 점은 학습을 통해 선형 함수의 회귀 최적선을 찾는 것이 아니라, 시그모이드 함수 최적선을 찾고 이 시그모이드 함수의 반환 값을 확류로 간주해 확률에 따라 분류를 결정한다는 것이다.
시그모이드 함수는 x값이 +, -로 아무리 커지거나 작아져도 y값은 항상 0과 1사이 값을 반환한다. x값이 커지면 1에 근사하며, x값이 작아지면 0에 근사한다.
로지스틱 회귀는 선형 회귀 방식을 기반으로 하되, 시그모이드 함수를 이용해 분류를 수행하는 회귀이다. 로지스틱 회귀는 가볍고 빠르지만 이진 분류 예측 성능도 뛰어나다. 이 때문에 로지스틱 회귀를 이진 분류의 기본 모델로 사용하는 경우가 많다. 또한 로지스틱 회귀는 희소한 데이터 세트 분류에도 뛰어난 성능을 보여서 텍스트 분류에도 자주 사용된다.
회귀 트리
회귀를 위한 트리를 생성하고 이를 기반으로 회귀 예측하는 것이다. 회귀 트리는 4장의 분류에서 배운 분류 트리와 크게 다르지 않다. 다만 리프 노드에서 예측 결정 값을 만드는 과정에 차이가 있는데 분류 트리가 특정 클래스 레이블을 결정 하는 것과는 달리 회귀 트리는 리프 노드에 속한 데이터 값의 평균값을 구해 회귀 예측값을 계산한다.
트리계열의 장점 : 설명이 쉽고, 데이터 전처리가 필요없다
트리계열의 단점 : 튜닝을 해도 드라마틱한 결과 X, 범위를 벗어난 값은 예측이 안됨, 성능이 잘 나올 수는 있는데 과적합 될 수 있다.
회귀 실습 - 자전거 대여 수요 예측
데이터 클렌징 및 가공과 데이터 시각화
rmsle( ) 함수를 만들 때 주의해야할 점 : rmsel를 구할 때 넘파이의 log( )함수를 이용하거나 사이킷런의 mean_squared_log_error( )를 이용할 수 있지만 데이터 값의 크기에 따라 오버플로/언더플로 오류가 발생하기 쉽다. 따라서 log( )보단 log1p( )를 이용하는데 log1p( )의 경우 1+log ( ) 값으로 log 변환 값에 1을 더하므로 이런 문제를 해결 해준다. 그리고 log1p( )로 변환된 값은 다시 넘파이의 expm1( )함수로 쉽게 원래 스케일로 복원 될 수 잇다.
로그 변환, 피처 인코딩과 모델 학습/예측/평가
회귀에서 이렇게 큰 예측 오류가 발생할 경우 가장 먼저 살펴볼 것은 Target 값의 분포가 왜곡된 형태를 이루고 있는지 확인 하는 것이다. Target 값의 분포는 정규 분포 형태가 가장 좋다. 그렇지 않고 왜곡 된 경우엔 회귀 예측 성능이 저하되는 경우가 발생하기 쉽다. 왜곡된 값을 정규 분포 형태로 바꾸는 일반적인 방법은 로그를 적용해 변환하는 것이다.(numpy의 log1p( ) 함수 이용) 변경된 Target 값을 기반으로 학습하고 예측한 값은 다시 expm1( )함수를 적용해 원래 scale 값으로 원상복구하면 된다.
사이킷런은 카테고리 피처만을 위한 데이터 타입이 없어 모두 숫자로 변환해야한다. 하지만 이처럼 숫자형 카테고리 값을 선형 회귀에 사용할 경우 회귀 계수를 연산할 때 이 숫자형 값에 크게 영향 받는 경우가 발생할 수 있다. 따라서 선형 회귀에서는 이러한 피처 인코딩에 원-핫 인코딩을 적용해 변환해야한다. 원-핫 인코딩을 통해서 피처들의 영향도가 달라졌고, 모델의 성능도 향상되었다. 반드시 그런건 아니지만 선형 회귀의 중요 카테고리성 피처들을 원-핫 인코딩으로 변환하는 것은 성능에 중요한 영향을 미칠 수 있다.
회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
데이터 사전 처리 (Preprocessing)
이상치를 찾는 것은 쉽지 않지만 회귀에 중요한 영향을 미치는 피처를 위주로 이상치 데이터를 찾으려는 노력은 중요하다. 대략의 데이터 가공과 모델 최적화를 수행한 뒤 다시 이에 기반한 여러 가지 기법의 데이터 가공과 하이퍼 파라미터 기반의 모델 최적화를 반복적으로 수행하는 것이 바람직한 머신러닝 모델 생성 과정이다. 다항 회귀도 선형 회귀이다. 선형/비선형 회귀를 나누는 기준은 회귀 계수가 선형/비선형인지를 따르는 것이다. 독립변수의 선형/비선형 여부와는 무관.
다항 회귀를 이용한 과소적합 및 과적합 이해
다항 회귀는 피처의 직선적 관계가 아닌 복잡한 다항 관계를 모델링 할 수 있다. 다항식의 차수가 높아질수록 매우 복잡한 피처 간의 관계까지 모델링이 가능하다. 하지만 다항 회귀의 차수를 높일 수록 학습 데이터에만 너무 맞춘 학습이 이뤄져 테스트 데이터 환경에서의 예측 정확도가 떨어지는 과적합 문제가 발생한다.
'Computer > Machine Learning' 카테고리의 다른 글
| CH6. 머신러닝 복습 : 차원 축소 (1) | 2023.06.07 |
|---|---|
| CH 4. 머신러닝 복습 : 분류 (0) | 2023.05.11 |
| Ch 3. 머신러닝 복습 : 평가 (0) | 2023.04.24 |
| Ch 2. 머신러닝 복습 : 사이킷런으로 시작하는 머신러닝 (0) | 2023.04.20 |
| Ch09. 추천 시스템 (0) | 2022.11.15 |


